Young Learners' Tangram House - a different STEM skills practice
- Jolly's Class

- 18.05.2022 г.
- време за четене: 3 мин.
Like building blocks, tangrams can teach kids about spatial relationships (how some object is located in space in relation to another). They may help kids learn geometric terms, and develop stronger problem solving abilities. They might even help children perform better on tests of basic arithmetic. But what is a tangram?
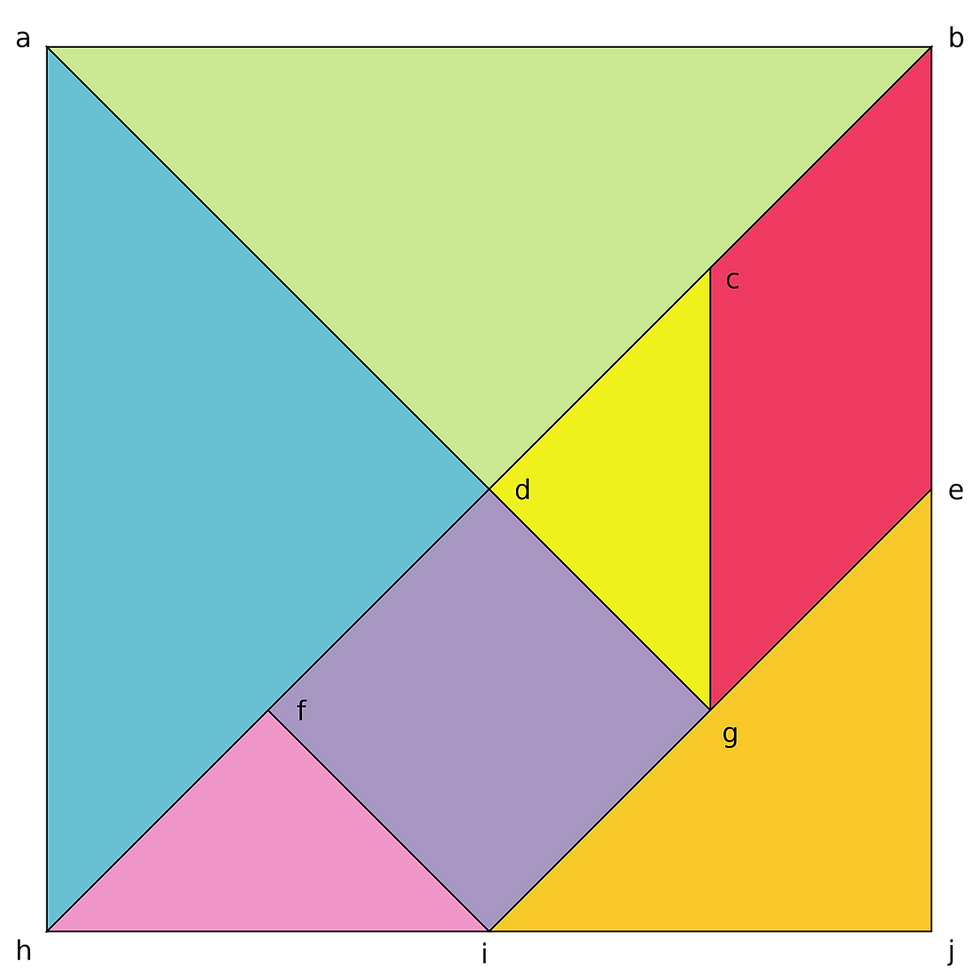
Invented in China approximately 200 years ago, a tangram is a two-dimensional re-arrangement puzzle created by cutting a square into seven pieces — seven geometric shapes called “tans”.
What are the seven shapes in a tangram? Each tangram puzzle contains the following:
2 large right triangles
1 medium-sized right triangle
2 small right triangles
1 small square
1 parallelogram
Arranged correctly, these tangram shapes can be fitted together as a large square, rectangle, or triangle. They can also be arranged in a variety of complex shapes, including unusual ones.
There are many ways to play with tangrams. The simplest way is to let kids create their own complex shapes. But traditionally, tangrams are treated as puzzles.
The player is shown a target shape in outline, so that the “seams” between the composite tans are concealed. Then the player attempts to recreate the shape using the seven pieces.

The educational benefits of tangrams
When we play with tans, we consider the shapes from a variety of angles and perspectives. How would the shapes look if we stuck them together? Rotated them? Slide them around into different positions?
Experiments suggest that thinking about such things — visualizing the spatial relationships between shapes in your “mind’s eye” — can boost our visual spatial relationships.
Research hints that it can boost arithmetic performance, too. When Yi Ling Cheng and Kelly Mix asked kids, aged 6-8, to perform a series of tangram-like spatial tasks, the practice session seemed to prime the brain for mathematics. Kids who spent 40 minutes solving shape rotation puzzles performed better on a pencil-and-paper arithmetic test immediately thereafter. Compared to tangram-like activities, crossword puzzle warm-ups had no such effect (Cheng and Mix 2012).
So there is reason to suspect that playing with tangrams has educational benefits, and many educators recommended their use in the classroom (Bohning and Althouse 1997; Krieger 1991; National Council of Teacher’s Mathematics 2003; Clements and Sarama 2014).
Today we share with you an idea for homemade tangram house which can be simply made of paper! You can download the resources from here!
In particular, tangrams may help kids
classify shapes
develop positive feelings about geometry
gain a stronger grasp of spatial relationships
develop an understanding of how geometric shapes can be decomposed
boost spatial rotation skills
acquire a precise vocabulary for manipulating shapes (e.g., “flip,” “rotate”)
learn the meaning of compatibility
But it’s not clear how many of these benefits will arise if a child plays with tangrams on his or her own, without any discussion or teamwork. Studies indicate that spatial play — like playing with tangrams — is particularly educational when kids interact with others who use spatial vocabulary.
For example, toddlers tend to develop bigger spatial vocabularies if, during play, their parents expose them to a greater range of spatial words, like “triangle” and “line.”
So it’s likely we can boost the value of tangrams by actively engaging kids in conversation. We can introduce them to words they might not know, like “angle” and “parallelogram.”
Any other teaching tips?
Tangrams offer kids an excellent opportunity to test out different geometric manipulations and become familiar with the properties of the shapes they use.
But notice the triangles– big, medium, and small — are all the same shape. They represent a special kind of right triangle — an isosceles triangle with two 45-degree angles, and one 90-degree angle. And if you put together two triangles of the same size, you can make a square.
These properties aren’t found in all triangles. On the contrary! But it’s easy for children to come to that conclusion if they don’t get exposed to a variety of triangles — equilateral, isosceles, and scalene. So it’s important to expose kids to that variety, and call their attention to the ways in which triangles can differ (Clement and Sarama 2014).




Comments